This page gives a list of works on the topic of Fokas' method, organised thematically. The list is growing and we hope to make it comprehensive soon. In the mean time, if you know of any omissions please send us an email with as much information as possible on the work.
To view the abstract for a work, you can hover the mouse over the word abstract appearing below the work's reference. Every effort has been made to ensure that the abstracts display clearly but if any are unclear please notify us.
Problems in two dimensions (either 1+1 or 2+0)
Linear evolution PDEs formulated on the half-line
The novel integral representations obtained by the new method have
both analytical and numerical advantages in comparison with the classical
integral and series representations: (i) They are uniformly convergent at the
boundaries; analytically, this makes it easier to prove rigorously the validity
of such representations without the apriori assumption of existence,
whereas numerically, using appropriate contour deformations, it makes it
possible to obtain integrands which decay exponentially as |k|
→∞ and this leads to efficient numerical computations
[FF2008a],
[KP2009a],
[Vet2010a].
(ii) These representations retain their form even for more complicated boundary
conditions, whereas the classical representations involve infinite series over
a spectrum determined by a transcendental equation. For example, in the case
of the heat equation with Robin boundary conditions, the classical
representation involves an infinite series over
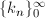 where
kn satisfy a transcendental equation, whereas the new
method yields an explicit integral representation.
where
kn satisfy a transcendental equation, whereas the new
method yields an explicit integral representation.
Linear evolution PDEs formulated on a finite interval
The new transform method yields integral representations for evolution PDEs containing x-derivatives of arbitrary order formulated on the finite interval [Fok2008a], whereas it can be shown that even for the linearised KdV on the finite interval with generic boundary conditions, there does not exist an infinite series representation [Pap2011a], [Smi2011a]! Note that some of the works listed descibing linear evolution PDEs formulated on the half-line also refer to finite interval formulations.
Linear evolution PDEs formulated in a time-dependent domain
The new method can be used to study linear evolution equations in domains of the form l(t)<x<∞, 0<t<T, with prescribed initial and boundary conditions and with l(t) a given differentiable function. In this case, the solution is characterised in general by a system of linear integral equations with explicit, weakly singular kernel. For example, for a second order problem such as the heat equation qt=qxx, given the Dirichlet boundary datum q(l(t),t), the unknown Neumann boundary value qx(l(t),t) can be computed as the solution of a single such linear Volterra integral equation.
Linear elliptic PDEs on the interior of a polygon
The new method yields novel integral representations for the solution of several classical PDEs including the Laplace, the Helmholtz, and the modified Helmholtz equations formulated in the interior of a convex polygon. These representations involve certain transforms of the associated boundary values. There now exist two global relations. For a simple domain, it is possible, using the global relations and their invariant properties, to express all transforms in terms of the given boundary conditions using only algebraic manipulations. For example, the solution of the Dirichlet problem for the modified Helmholtz equation in the interior of an equilateral triangle is expressed in terms of an integral in the complex k-plane which involves an integrand which decays exponentially as |k| →∞. This solution has analytical and numerical advantages in comparison with the classical series solution of Lamé; furthermore, problems with more complicated boundary conditions (for which the classical approach apparently fails) can also be solved in a similar way. For more complicated domains, the global relation provides novel effective numerical techniques for the determination of the unknown boundary values [FFSS2009a], [FSS2010a], [FFSS2008a], [FF2011a], [FS2009a] and [FFX2004a]. Several boundary value problems for the biharmonic equation are analysed in [CF2004a] and [DF2011a].
Linear elliptic PDEs in polar coordinates
The new method has also been implemented in the case of boundary value problems formulated in polar coordinates, and in particular has produced: (a) novel integral representations for the Poissonand Helmholtz equations, and (b) the solutions of several boundary value problems for these equations.
Spectral theory for non-self-adjoint boundary value problems
The new method permits investigation of initial-boundary value problems on rectangular domains without a priori assumptions on the eigenfunctions of the spatial differential operator. Moreover, the global relation may be used to determine the eigenfunctions directly and the methods of spetral theory applied to test their completeness and basic properties.
Linear elliptic PDEs on the exterior of a polygon
Linear and integrable nonlinear hyperbolic PDEs
Boundary value problems for these equations are simpler than boundary value problems for evolution and elliptic PDEs because all boundary values needed for the solution representation are prescribed as boundary conditions.
Integrable nonlinear evolution PDEs formulated on the half-line
The new method yields novel integral representations formulated in the complex k-plane (the Fourier plane). These integrals, in addition to the exponentials which appear in the integrals of the linearized version of these nonlinear PDEs, also contain the entries of a matrix-valued function M(x,t,k), which is the solution of a matrix Riemann-Hilbert (RH) problem. This RH problem is uniquely defined in terms of appropriate nonlinear transforms of boundary values, called spectral functions. These functions are defined in the Fourier space, i.e. they do not involve the independent variables of the PDE. This crucial feature of the new method makes it possible to obtain useful asymptotic information about the solution even before characterising the spectral functions in terms of the given boundary conditions. This can be achieved by using the Deift-Zhou (for the long-time asymptotics) [DZ1992a], [DZ1993a] and the Deift-Zhou-Venakides (for the zero-dispersion limit) [DVZ1994a], [DVZ1997a] techniques for the asymptotic analysis of these RH problems [Kam2003a], [FI1992a], [FI1996a], [FI1992b] and [FI1994a]. For certain nonlinear boundary value problems, called linearisable, it is possible, by analysing the global relation, to express the spectral functions in terms of the given initial and boundary conditions using only algebraic manipulations. Thus, for linearisable boundary conditions, the new method yields a representation which is as effective as the classical representation for the Cauchy problem obtained by the inverse scattering transform method. For general, non-linearisable boundary conditions the global relation yields an effective characterisation of the generalised Dirichlet to Neumann map. This important development was first achieved in [BFS2003a] by employing the so-called Gelfand-Levitan-Marchenko (GLM) representations [BK2000a], and was implemented numerically in [Zhe2006a] and [Zhe2007a]. It was later realised that this approach also provides a direct characterisation of the spectral functions in terms of the given initial and boundary conditions, bypassing the GLM representation, [Fok2005a] and [FT2008a]. Further progress in this problem was achieved in [FL2011b], where the relevant formulae were obtained without the need to introduce the GLM representations. However, it must be noted that for non-linearisable boundary value problems, the above characterisation involves a nonlinear equation.
Integrable nonlinear evolution PDEs on the finite interval
The most interesting aspect of this class of problems is the realization
that the
Integrable nonlinear elliptic PDEs formulated in the interior of a polygon
The new method again yields novel integral representations in the complex k-plane. These integrals, in adddition to the exponentials which appear in the integrals of the linearised versions of these nonlinear PDEs, also contain the entries of a matrix-valued function M(x,y,k) which is the solution of a matrix RH problem. The spectral functions, i.e. the entries of the relevant jump matrix which depend only on k, can be computed in terms of the associate boundary values. For elliptic PDEs involving only second order derivatives, by employing the two relevant global relations, it is possible to express the unknown boundary values via a system of nonlinear Fredholm integral equations. However, for linearisable boundary conditions, it is again possible to avoid this nonlinear step and to express the spectral functions directly in terms of the given boundary conditions. The new method has already been implemented to the elliptic sine-Gordon formulated in the quarter plane and in a semistrip, as well as to the celebrated Ernst equation formulated in several complicated domains. Furthermore, particular linearisable boundary value problems have been solved for these two physically significant PDEs.
Problems in three dimensions
Linear evolution PDEs in two space variables
The Fokas method has been applied to simple domains such as the quarter plane, as well as to more complicated domains such as the interior of the isosceles triangle.
Linear elliptic PDEs in spherical coordinates
The new method has also been implemented in the case of boundary value problems formulated in spherical coordinates and, in particular, has produced: (a) the classical Poisson integral formula for the solutions of the Dirichlet problem for the Poisson equation in the interior of a sphere, the analogous formula for the Neumann problem, and the generalisations of these formulae to n dimensions, (b) the solutions of various boundary value problems for the inhomogeneous Helmholtz equation in the interior of a sphere, and (c) the solution of the Dirichlet problem for the Laplace equation in the interior of a spherical sector.
Linear elliptic PDEs with nonlocal boundary conditions
In particular, the Fokas method has been applied to the problem of water waves, which involves the Laplace equation in three dimensions supplemented with certain nonlocal boundary conditions. This has led to a novel nonlocal formulation of this classical problem.
Quaternion methods
Elasticity and fluid loaded plate
The Fokas method yields novel results for the classical boundary value problems arising in elasticity and in fluid loaded plate in 2 and in 3 dimensions.
Nonlinear evolution PDEs in two spatial dimensions
The new method uses either a d-bar formalism (as in the case of the Davey-Stewartson (DS) equation), or a combination of the a d-bar formalism with a nonlocal Riemann-Hilbert formalism (as in the case of the Kadomtsev-Petviashvili (KP) equation), to produce novel integral representations together with the associated global relations. These representations depend on certain spectral functions which themselves are characterized via certain linear integral equations of Fredholm type in terms of the initial conditions and all the boundary values. The characterization of the spectral functions in terms of the given initial and boundary conditions remains open. Moreover, the question of identifying linearisable boundary conditions for the DS or the KP also remains open.
Differential-difference equations
Linear and integrable nonlinear differential-difference equations
Following the development of the Fokas method for PDEs, it has been shown that the method can also be used for solving differential-difference equations (DDEs) on the natural numbers. These equations can be considered as discrete analogues of IBVPs for PDEs, since lattice spacing are taken from the natural numbers instead of the integers. The new method can deal with IBVPs for discrete linear and integrable discrete nonlinear Schrödinger equations (also known as the Ablowitz-Ladik system [AL1975a], [AL1976a]) on the natural numbers [BH2008a]. Linearizable BCs for the integrable discrete nonlinear Schrödinger equation were analysed, which are the discrete analogue of the homogenous Robin-type BCs. When such BCs are given, the unknown boundary values can be eliminated using only algebraic manipulation of the global relation as shown in continuum problems. It is worth emphasizing that the Fokas method can be generalized to solve IBVPs for any discrete linear evolution equations with more general boundary conditions just as effectively [BW2010a]; this is to be contrasted with the classical Fourier series approach which is very limited.







 , which in turn are defined in terms of q0(x), {g0(t), g1(t)}, and {f0(t), f1(t)}, respectively.
, which in turn are defined in terms of q0(x), {g0(t), g1(t)}, and {f0(t), f1(t)}, respectively. . Hence, it is possible to evaluate this integral numerically in an efficient and straightforward manner. Other types of boundary value problems, including the Neumman and Robin problems, can be solved similarly.
. Hence, it is possible to evaluate this integral numerically in an efficient and straightforward manner. Other types of boundary value problems, including the Neumman and Robin problems, can be solved similarly. . The numerical method is based on the reduction of this problem to a lower-dimensional computation involving surface variables alone. To accomplish this, we describe the Taylor expansion of the Dirichlet Neumann operator in homogeneous powers of the surface elevation η. Each term is a concatenation of Fourier multipliers with powers of η and its derivatives and is valid uniformly in wavenumber. These are easily calculated using the fast Fourier transform. The method is illustrated by computing the long time evolution of modulated wave packets and of approximations to the Stokes steady wave train. By imposing a surface pressure we observe surface steepening in large amplitude evolution, and wake and bow wave development for flows with a close to critical Froude number. Finally, we give an example of nonlinear evolution of the distribution of energy among normal modes.
. The numerical method is based on the reduction of this problem to a lower-dimensional computation involving surface variables alone. To accomplish this, we describe the Taylor expansion of the Dirichlet Neumann operator in homogeneous powers of the surface elevation η. Each term is a concatenation of Fourier multipliers with powers of η and its derivatives and is valid uniformly in wavenumber. These are easily calculated using the fast Fourier transform. The method is illustrated by computing the long time evolution of modulated wave packets and of approximations to the Stokes steady wave train. By imposing a surface pressure we observe surface steepening in large amplitude evolution, and wake and bow wave development for flows with a close to critical Froude number. Finally, we give an example of nonlinear evolution of the distribution of energy among normal modes.